
Dieses "Nicht-Muster" hätte sicher auch Einstein gefallen.
Hobby-Mathematiker löst Rätsel um kuriose "Einstein-Form"
Dieser Artikel ist älter als ein Jahr!
Die Aufgabe ist einfach: Eine Fliese soll eine bestimmte Form haben, sodass sie niemals ein Muster wiederholt – egal, über wie viel Fläche sie verlegt wird. Die Lösung auf dieses Rätsel führte bisher bei Mathematiker*innen allerdings zu Kopfzerbrechen.
In der Mathematik bezeichnet man solche Fliesen als "aperiodische Monokacheln", im Englischen auch als "Einstein" bekannt. Mit dem berühmten Physiker hat die Form nichts zu tun. Vielmehr ist es ein Wortspiel mit den Wörtern "Ein" und "Stein", bezeichnet also "eine (einzelne) Kachel".
Bisher mindesten 2 Formen nötig
In den vergangenen 60 Jahren schritt die Forschung an diesen Einstein-Formen immer weiter voran, am nächsten kam man dem Muster in den 1970er-Jahren. Der Physik-Nobelpreisträger Roger Penrose fand Fliesenpaare, die Muster bilden konnten, die sich niemals wiederholten. Mit einer einzigen Kachel ließ sich das Problem allerdings nicht lösen.
Bis sich der englische Hobbymathematiker David Smith dem Problem annahm und der Einstein-Form auf der Spur kam. Die 13-seitige Form taufte er "den Hut", bei seinen ersten Versuchen schnitt er 32 Stück aus Karton aus und legte sie aneinander. Als er sah, dass er der Lösung auf der Spur war, informierte er Craig Kaplan, einen Informatikprofessor an der Universität von Waterloo in Kanada.
Ganze Gruppe von Einstein-Formen entdeckt
Gemeinsam mit einem Mathematiker und einem Software-Entwickler konnten sie beweisen, dass es sich bei "dem Hut" tatsächlich um eine Einstein-Form handelte. Und nicht nur das: Smith fand eine weitere Form, die an den Hut angelehnt ist und die Voraussetzungen einer Einstein-Form erfüllt: "die Schildkröte".
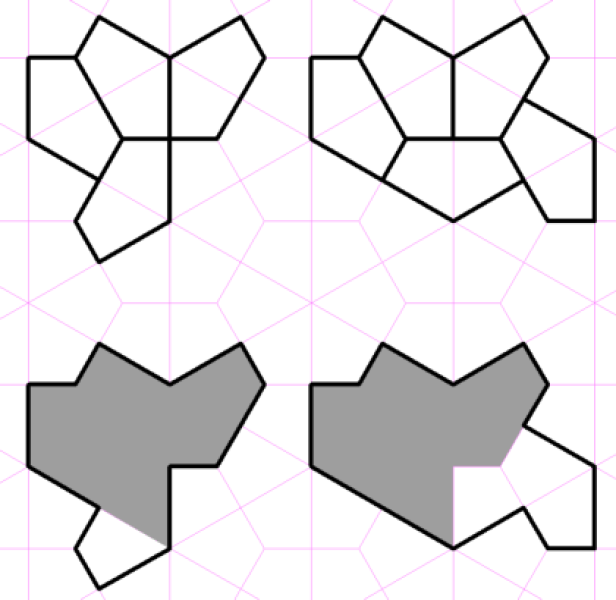
Der Hut (links) und die Schildkröte (rechts).
© David Smith
Ihre Ergebnisse machten die Forscher in einem Paper öffentlich, das bisher allerdings noch nicht von der Forschungsgemeinschaft überprüft wurde. Sie sind sich allerdings sicher, dass sie auf eine gesamte Klasse an Einstein-Formen gestoßen sind.
Inwiefern diese Formen auch außerhalb der Welt der Mathematik Anwendungen finden, muss man noch herausfinden. Kaplan ist sich sicher, dass es "viele Anwendungen in der Kunst, Design und Architektur gibt". Auch zur Erforschung von Quasikristallen könnten die Einstein-Formen nützlich sein.
"Zunächst stellt sich aber die Frage, wer der erste ist, der ein Foto von seinem Badezimmer macht, das mit den Hüten gefliest wurde", sagt Kaplan gegenüber dem Guardian. Keksausstecher gibt es immerhin schon.



Kommentare